Central limit theorem citaat information
Home » Trending » Central limit theorem citaat informationYour Central limit theorem citaat images are available in this site. Central limit theorem citaat are a topic that is being searched for and liked by netizens now. You can Find and Download the Central limit theorem citaat files here. Find and Download all free images.
If you’re looking for central limit theorem citaat pictures information linked to the central limit theorem citaat keyword, you have come to the ideal blog. Our site frequently provides you with hints for viewing the maximum quality video and image content, please kindly hunt and find more informative video articles and graphics that match your interests.
Central Limit Theorem Citaat. This theorem is an enormously useful tool in providing good estimates for probabilities of events depending on either s n or x¯ n. So the random variable (x ˉ n − μ) will converge to zero. Proof of the central limit theorem we have n independent and identical random variables x 1 to x n. The central limit theorem states that the sum of a number of independent and identically distributed random variables with finite variances will tend to a normal distribution as the number of variables grows.
 Statistics Lecture 8.2 Central Limit Theorem and From youtube.com
Statistics Lecture 8.2 Central Limit Theorem and From youtube.com
The central limit theorem (clt) is one of the most popular theorems in statistics and it’s very useful in real world problems. In other words, the central limit theorem is exactly what the shape of the. This theorem is an enormously useful tool in providing good estimates for probabilities of events depending on either s n or x¯ n. Using the central limit theorem, a variety of parametric tests have been developed under assumptions about the parameters that determine the population probability distribution. So the random variable (x ˉ n − μ) will converge to zero. We shall begin to show this in the following examples.
Central limit theorem lisa yan and jerry cain october 23, 2020 1 cs109:
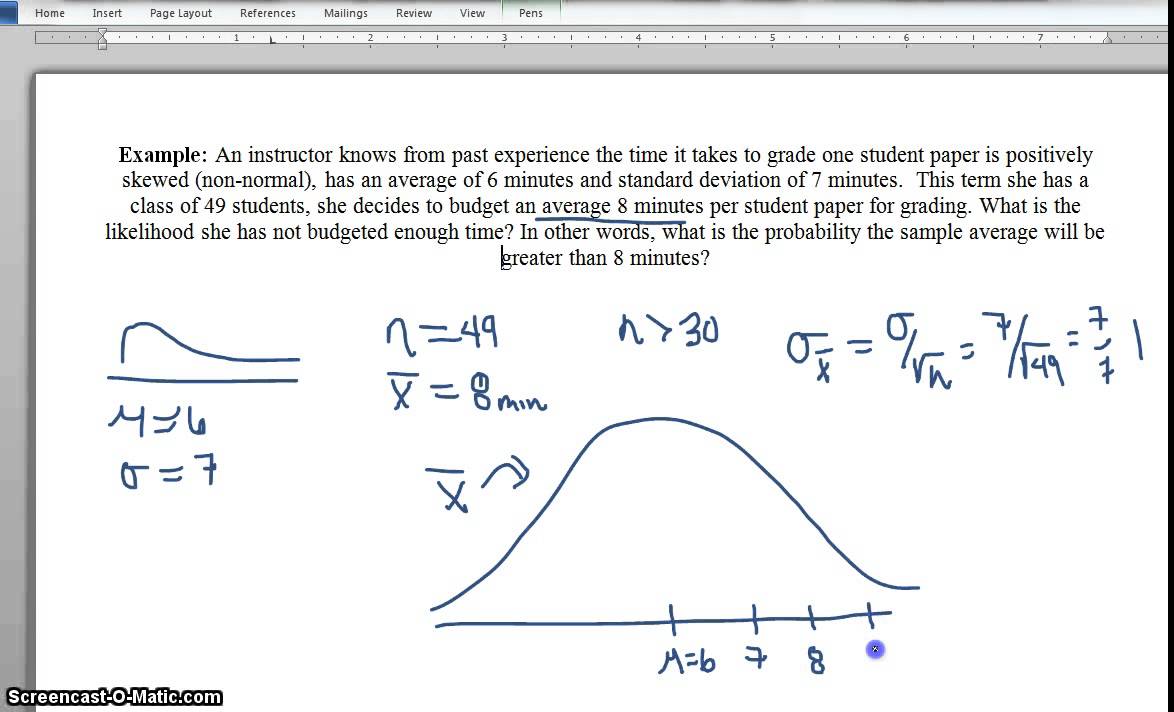
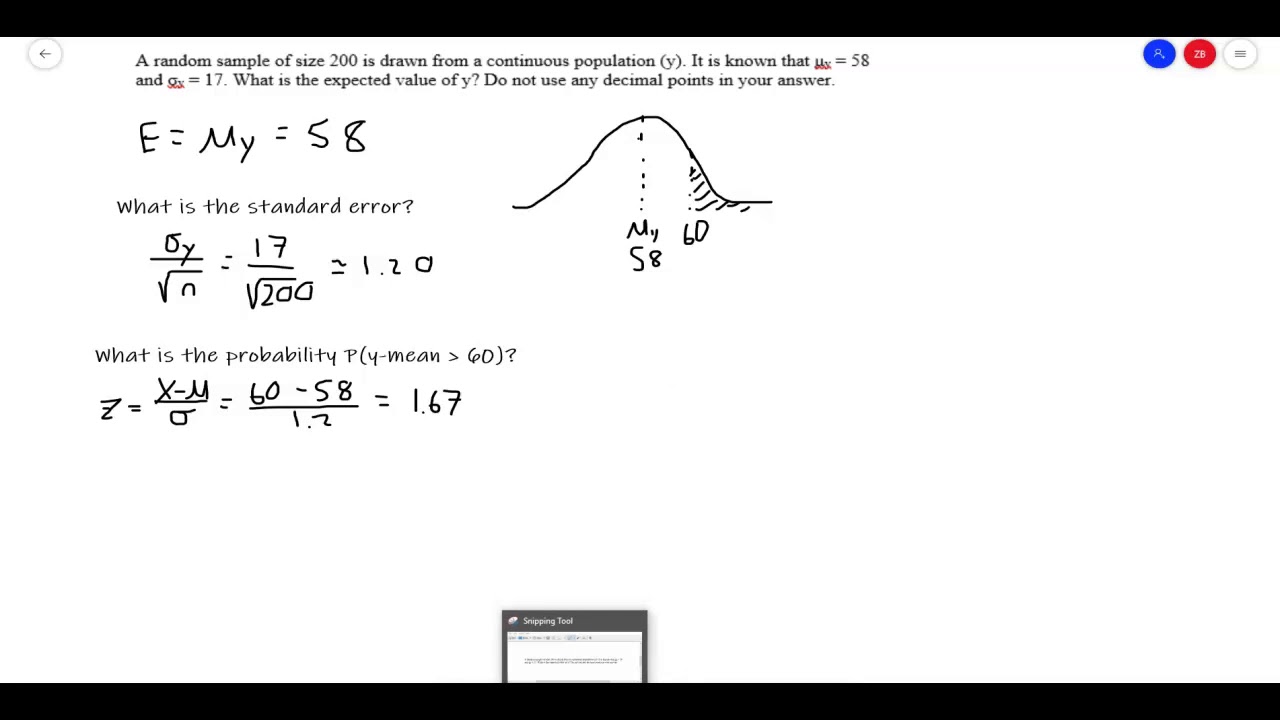
If it asks about a single observation, then do not try to use the central limit theorem. According to the central limit theorem, the means of a random sample of size, n, from a population with mean, µ, and variance, σ 2, distribute normally with mean, µ, and variance, σ 2 n. The central limit theorem summary the theorem how good is the clt approximation? Using the central limit theorem, a variety of parametric tests have been developed under assumptions about the parameters that determine the population probability distribution. 1 central limit theorem what it the central limit theorem? Central limit theorem is a statistical theory which states that when the large sample size is having a finite variance, the samples will be normally distributed and the mean of samples will be approximately equal to the mean of the whole population.
 Source: youtube.com
Source: youtube.com
This formula points out that the distribution of the sample has the following central limit theorem conditions: The sample mean will approximately be normally distributed for large sample sizes, regardless of the distribution from which we are sampling. If it asks about a single observation, then do not try to use the central limit theorem. A problem may ask about a single observation, or it may ask about the sample mean in a sample of observations. So the random variable (x ˉ n − μ) will converge to zero.
 Source: towardsdatascience.com
Source: towardsdatascience.com
The central limit theorem states that the sampling distribution of a sample mean is approximately normal if the sample size is large enough, even if the population distribution is not normal. De ne now the sample mean and the total of these nobservations as follows: We shall begin to show this in the following examples. The samples must be independent Central limit theorem (clt) is commonly defined as a statistical theory that given a sufficiently large sample size from a population with a finite level of variance, the mean of all samples from the same population will be approximately equal to the mean of the population.
 Source: youtube.com
Source: youtube.com
In a lot of situations where you use statistics, the ultimate goal is to identify the characteristics of a population. This theorem explains the relationship between the population distribution and sampling distribution. Using the central limit theorem, a variety of parametric tests have been developed under assumptions about the parameters that determine the population probability distribution. Μ x ¯ = μ = 1 2. This theorem is an enormously useful tool in providing good estimates for probabilities of events depending on either s n or x¯ n.
 Source: youtube.com
Source: youtube.com
De ne now the sample mean and the total of these nobservations as follows: This theorem explains the relationship between the population distribution and sampling distribution. The central limit theorem also states that the. If it asks about a single observation, then do not try to use the central limit theorem. Central limit theorem is a statistical theory which states that when the large sample size is having a finite variance, the samples will be normally distributed and the mean of samples will be approximately equal to the mean of the whole population.
 Source: youtube.com
Source: youtube.com
The central limit theorem for sample means (averages) in a population. In this article we’ll see why the central limit theorem is so useful and how to apply it. According to central limit theorem, for sufficiently large samples with size greater than 30, the shape of the sampling distribution will become more and more like a normal distribution, irrespective of the shape of the parent population. De ne now the sample mean and the total of these nobservations as follows: Central limit theorem (clt) is commonly defined as a statistical theory that given a sufficiently large sample size from a population with a finite level of variance, the mean of all samples from the same population will be approximately equal to the mean of the population.
 Source: youtube.com
Source: youtube.com
Letting x denote the mean of all nrandom variables, p n x ˙!d n(0;1) the notation !d is read \converges in distribution to, and In practical terms the central limit theorem states that p{a<z n b}⇡p{a<z b} =(b)(a). The sample mean is given by x ˉ n = n x 1 + x 2 + x 2 + ⋯ + x n the sample mean will converge to the population mean μ as n → ∞ (this is the law of large numbers). In probability theory, the central limit theorem (clt) states that the distribution of a sample variable approximates a normal distribution (i.e., a. Now, our end goal is to compare the normal distribution, as defined by the clt, to the actual distribution of the sample mean.
 Source: youtube.com
Source: youtube.com
Certain conditions must be met to use the clt. For reference, here is the density of the normal distribution n( ;˙2) with mean and variance ˙2: Using the central limit theorem, a variety of parametric tests have been developed under assumptions about the parameters that determine the population probability distribution. In probability theory, the central limit theorem (clt) states that the distribution of a sample variable approximates a normal distribution (i.e., a. The central limit theorem states that if the sample size is large enough, even if the population distribution is abnormal, the sample mean distribution will be approximately normal.
 Source: youtube.com
Source: youtube.com
In other words, the central limit theorem is exactly what the shape of the. X = p n i=1 x i n t= xn i=1 x i For reference, here is the density of the normal distribution n( ;˙2) with mean and variance ˙2: It states that, under certain conditions, the sum of a large number of random variables is approximately normal. Here, we state a version of the clt that applies to i.i.d.
 Source: youtube.com
Source: youtube.com
In other words, the central limit theorem states that for any population with mean and standard. Regardless of the population distribution model, as the sample size increases, the sample mean tends to be normally distributed around the population mean, and its standard deviation shrinks as n increases. In a lot of situations where you use statistics, the ultimate goal is to identify the characteristics of a population. This theorem is an enormously useful tool in providing good estimates for probabilities of events depending on either s n or x¯ n. Now, our end goal is to compare the normal distribution, as defined by the clt, to the actual distribution of the sample mean.

Here, we state a version of the clt that applies to i.i.d. For bernoulli random variables, µ = p and = p p(1p). Μ x ¯ = μ = 1 2. If it asks about a single observation, then do not try to use the central limit theorem. The central limit theorem for means the central limit theorem for means describes the distribution of x in terms of , ˙, and n.
.png “Central limit theorem? Socratic”) Source: socratic.org
In other words, the central limit theorem is exactly what the shape of the. Μ x ¯ = μ = 1 2. The central limit theorem states that the sum of a number of independent and identically distributed random variables with finite variances will tend to a normal distribution as the number of variables grows. 1 central limit theorem what it the central limit theorem? In a lot of situations where you use statistics, the ultimate goal is to identify the characteristics of a population.
 Source: youtube.com
Source: youtube.com
The central limit theorem was first established within the framework of binomial distribution by moivre, abraham de (1733).laplace, pierre simon de (1810) formulated the proof of the theorem. Now, our end goal is to compare the normal distribution, as defined by the clt, to the actual distribution of the sample mean. According to central limit theorem, for sufficiently large samples with size greater than 30, the shape of the sampling distribution will become more and more like a normal distribution, irrespective of the shape of the parent population. A problem may ask about a single observation, or it may ask about the sample mean in a sample of observations. In this article we’ll see why the central limit theorem is so useful and how to apply it.
 Source: slideshare.net
Source: slideshare.net
In practical terms the central limit theorem states that p{a<z n b}⇡p{a<z b} =(b)(a). The central limit theorem (clt) is one of the most popular theorems in statistics and it’s very useful in real world problems. Μ x ¯ = μ = 1 2. The sample mean is given by x ˉ n = n x 1 + x 2 + x 2 + ⋯ + x n the sample mean will converge to the population mean μ as n → ∞ (this is the law of large numbers). De ne now the sample mean and the total of these nobservations as follows:
 Source: youtube.com
Source: youtube.com
The central limit theorem states that if the sample size is large enough, even if the population distribution is abnormal, the sample mean distribution will be approximately normal. In practical terms the central limit theorem states that p{a<z n b}⇡p{a<z b} =(b)(a). In a lot of situations where you use statistics, the ultimate goal is to identify the characteristics of a population. Μ x ¯ = μ = 1 2. Central limit theorem lisa yan and jerry cain october 23, 2020 1 cs109:
 Source: youtube.com
Source: youtube.com
The central limit theorem (formal) central limit theorem: Here, we state a version of the clt that applies to i.i.d. The sample mean is given by x ˉ n = n x 1 + x 2 + x 2 + ⋯ + x n the sample mean will converge to the population mean μ as n → ∞ (this is the law of large numbers). Proof of the central limit theorem we have n independent and identical random variables x 1 to x n. The central limit theorem, therefore, tells us that the sample mean x ¯ is approximately normally distributed with mean:
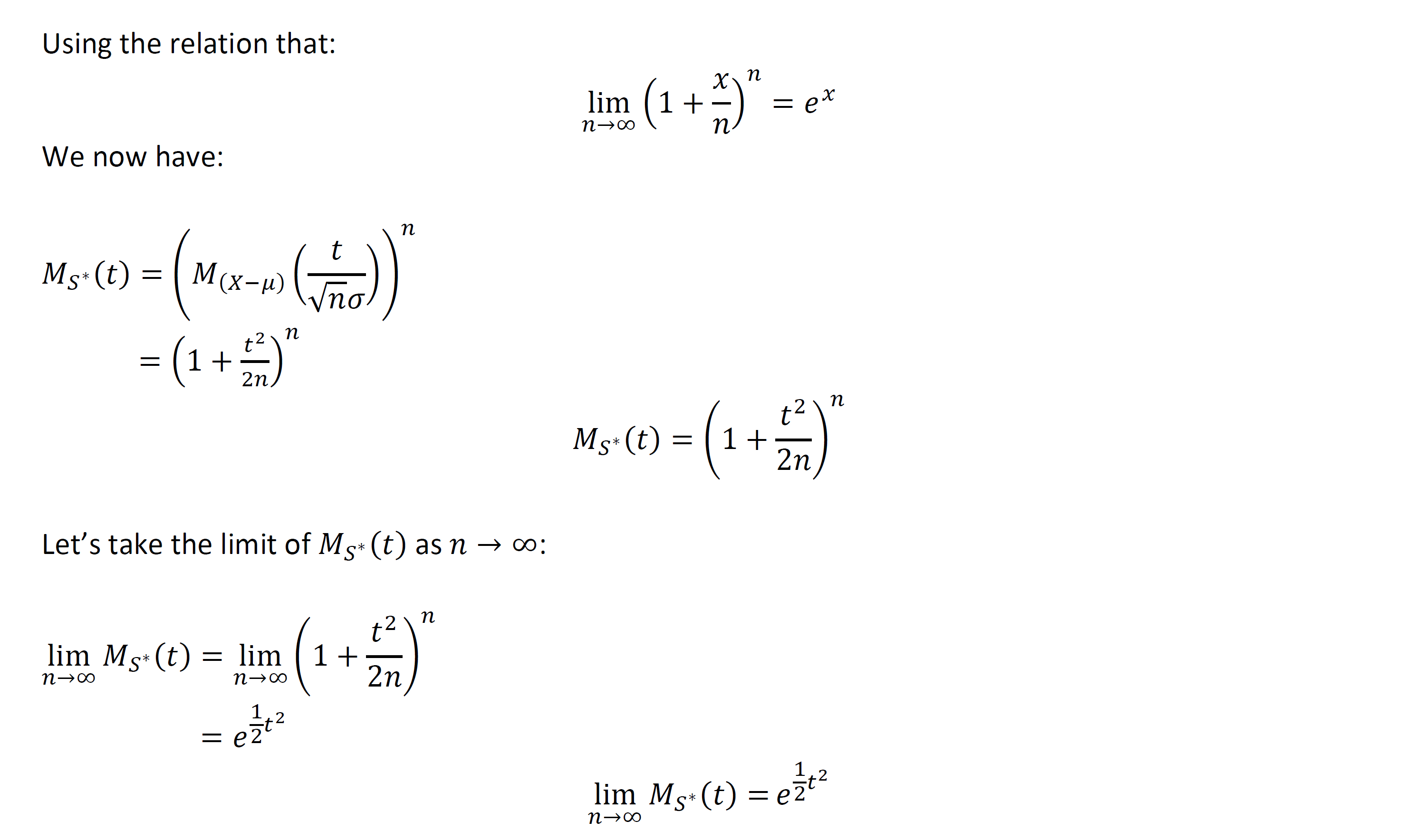 Source: towardsdatascience.com
Source: towardsdatascience.com
The central limit theorem, therefore, tells us that the sample mean x ¯ is approximately normally distributed with mean: Regardless of the population distribution model, as the sample size increases, the sample mean tends to be normally distributed around the population mean, and its standard deviation shrinks as n increases. In other words, the central limit theorem states that for any population with mean and standard. The central limit theorem states that if the sample size is large enough, even if the population distribution is abnormal, the sample mean distribution will be approximately normal. It states that, under certain conditions, the sum of a large number of random variables is approximately normal.
 Source: youtube.com
Source: youtube.com
The sample mean is given by x ˉ n = n x 1 + x 2 + x 2 + ⋯ + x n the sample mean will converge to the population mean μ as n → ∞ (this is the law of large numbers). Proof of the central limit theorem we have n independent and identical random variables x 1 to x n. In other words, the central limit theorem states that for any population with mean and standard. The central limit theorem also states that the. The central limit theorem for sample means (averages) in a population.
 Source: youtube.com
Source: youtube.com
The central limit theorem states that the sum of a number of independent and identically distributed random variables with finite variances will tend to a normal distribution as the number of variables grows. The central limit theorem suppose that a sample of size nis selected from a population that has mean and standard deviation ˙. This formula points out that the distribution of the sample has the following central limit theorem conditions: Here, we state a version of the clt that applies to i.i.d. 1 central limit theorem what it the central limit theorem?
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site value, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title central limit theorem citaat by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
Category
Related By Category
- Autonomie citaten information
- Apa citation maker website information
- 10 citate despre iubire information
- 2018 journal citation reports information
- Blik op de weg citaat information
- Belle citation courtes information
- Baudelaire citation information
- Apa citation sample book information
- Aya ezawa google citations information
- Apa citation generator for government website information